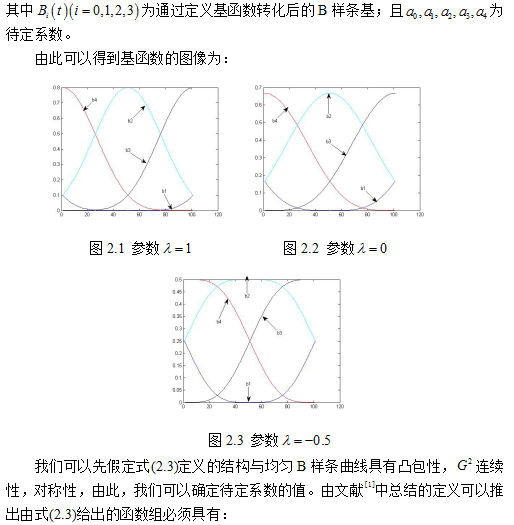
对于连续性而言，无论是三角Bézier曲线还是三角B样条曲线，在满足不同的条件时，其连续性的意义也不尽相同。对于曲线来说，使用范围更为广泛的是本文将在下面讨论的几何连续，通过参考多项式函数重新以三角函数为基础定义新的可调类Bézier曲线，在一个参数的基础上，通过分析曲线的基函数和性质，讨论了连续的条件和几何意义。

第三章小结

本章在给出了3次三角Bézier曲线的可调类之间的连续的拼接定理，在定义了曲线的基函数的基础上，验证其端点性质，在根据其端点性质，分别论证其他定理，其中曲线连续性的验证主要依据了几何不变性，保凸性，和端点性质等，通过拼接，曲线可以实现更多设计需要，实现更多设计功能，因此，曲线的G系列连续相比参数连续，具有更广泛的应用前景。

基于Bézier曲线的方法和B样条方法不能准确地代表圆锥曲线抛物线，并且只能通过修改控制点调整曲线的形状很不不便，很多研究虽然进行了讨论。但之前一些文献里的对Bézier方法或B样条方法的改进，除了关注如何构建定义的过渡函数曲线可以代表一些圆锥曲线或超越曲线，或在不能改变控制点的情况下自由地调整目标的形状。大多数文献对于讨论构造曲线的基本性质并不全面，如凸包、对称、几何不变性，对于这些就像三角Bézier曲线和均匀B样条曲线一样，有相同的变差缩减性，仿射不变性，保形性，因此只是适合曲线设计，但却很少可以讨论。考虑传统建模方法改进的不便，同时，也考虑到三角Bézier曲线和均匀B样条曲线的变差缩减性，可以通过改变形参值不改变点的情况下进行优化。本文在基函数的确定以后，主要运用新的转化基函数重新定义曲线，通过新定义的曲线主要用它实现曲线的C连续，并由曲线推广到了曲面的设计和椭圆的实现。

本文在参考阅读了大量文献的基础上，把论文侧重点选在了基函数的构造和转化以及曲线曲面的设计方面，因此，在以后的工作中，还是有一些问题需要继续深入研究和验证的，比如说，由曲线想曲面扩展时分片曲线到曲面的控制点选取，参数影响和实际拼接问题，同时需要考虑能否使用不同的定义方式来构造需求的三次曲面，当然虽然想法很多，但是限于目前的水平和相关知识的短板，无法有效做到，希望在以后的学习中，可以找到更好的解决办法