几个双邻接冠图的无符号拉普拉斯谱

本节为大家介绍几种不同的邻接双冠的无符号拉普拉斯谱。 获得的结果的证明与上一节中获得的结果非常相似。 这里考虑超邻接冠状矩阵。以下结果描述了细分双邻域冠状图的所有无符号拉普拉斯特征值。

定义4.2.1：令为n个顶点和m个边的r-正则图。 让和分别在和个顶点上的任何两个图形。然后无符号拉普拉斯的谱由下面的多项式组成：

一种图操作的基尔霍夫指数

在这一章中，我们首先先引入一种图操作，并推导它的无符号拉普拉斯特征多项式。然后推导了这些图操作的基尔霍夫指数，研究这些无符号拉普拉斯多项式和原图特征多项式的关系。

相关背景与概念

在一些图论问题中, 往往要计算一些图操作后的图谱问题.  许多图操作后的“导出图”的谱与“原图”的谱之间的关系得到了刻画, 如,线图, 细分图, 全图等。研究简单图经过图操作后的“导出图”的基尔霍夫指数指数是个非常有趣的问题。他们得到了正则图的线图, 细分图, 全图的基尔霍夫指数公式和上下界。在文献[15]中,王维忠等决定了正则图的操作和操作的拉普拉斯多项式, 并推导了这些图的基尔霍夫指数公式和上下界。受上面的研究结果的启发,在这一章, 我们在图操作的基础上引进了一种图操作, 并推导了其拉普拉斯特征多项式。

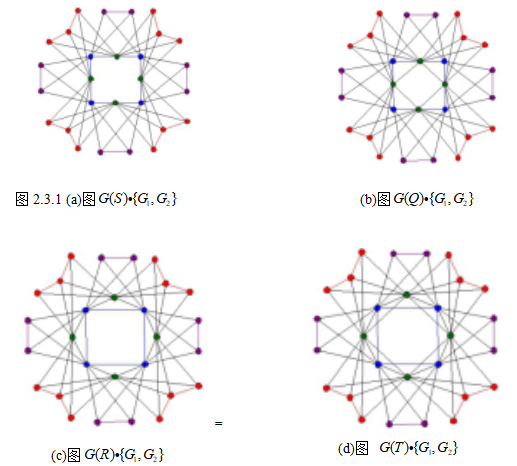
定义 5.1.1 ：设R(G) = (V (R(G)); E(R(G))) 是由图经“对应的每一条边添加一个新的顶点，且连接与其对应边 的两个端点”所得到的图(见图5.1 (a) 和(b))。

本文研究的主要成就

本文首先定义了许多冠图以及它的变形的操作，其次定义了两种矩阵（超冠矩阵和超邻接冠矩阵），然后我们计算了前面几种冠图以及他们变形操作下的无符号拉普拉斯谱。最后我们定义了操作，研究在操作之下的无符号拉普拉斯多项式和原图特征多项式的关系以及操作下的无符号拉普拉斯谱。

本文的创新点

本文中研究一些图操作下的无符号拉普拉斯谱，而不是近期研究比较热门的拉普拉斯谱、邻接谱和规范拉普拉斯谱，这在我们研究图的无符号拉普拉斯谱的方面提供了许多数据和理论支持。

论文总结

虽然描述拉普拉斯谱的技术只是猜测矩阵的特征向量，但它具有优于其他技术的优点，他可以描述所有冠状图特征向量与特征值。我们可以通过假设，，我们可以看出，任何冠图的无符号拉普拉斯矩阵是超冠矩阵。因此，可以从超冠矩阵的谱中容易地获得冠图的非零拉普拉斯特征值。可以对边冠图进行类似的假设。因此，可以说新的冠图的变形操作更广泛。由于非零拉普拉斯特征值的乘积与图中生成树的数量直接相关，可以容易地获得表达式以确定几个双冠图的生成树数。如果我们选择G和H作为一对非同构拉普拉斯......