常微分方程解的存在性定理及应用
[关键词:常微分方程,存在性定理] [热度 ]| 提示:此毕业设计论文完整版包含【论文】 作品编号:jskx0265,word全文:25页,合计:11000字 |

微分方程解的存在性理论是求解常微分方程的必要条件,该理论也是常微分方程的基础理论之一。本文主要研究常微分方程解的存在唯一性定理,并且在解的唯一性上给出奇解与包络证明,以及类似证明了线性微分方程组与高阶线性微分方程解的存在唯一性定理,最后介绍常微分方程在数学建模和数值计算中的应用。
本文的课题为“常微分方程解的存在性定理及应用”,通过该课题对常微分方程理论基础——微分方程解的存在性定理,以及常微分方程应用方面的介绍,如:微分方程解的存在性定理及证明、微分方程的特殊解——奇解与包络、线性微分方程组和高阶线性微分方程解的存在性定理证明,和常微分方程的应用——常微分方程模型的数学建模与常微分方程的数值计算等,了解到掌握数学方面理论知识,能够更好的结合实际应用解决问题。常微分方程解的存在性定理是求解微分方程的基础,同时也是研究更为复杂的微分方程的基础,而奇解与包络也是对微分方程解的存在唯一性研究得出的。通过更好的了解和掌握这方面数学理论,才能将理论数学转化为应用数学,例如数学建模的简单应用,结合计算机分析求解常微分方程的数值解。
本文通过介绍了微分方程解的存在性理论,以及常微分方程的应用方面内容。在微分方程解的存在性理论中,证明了一阶微分方程满足初值条件下的解的存在性唯一性定理,并且在该定理的唯一性方面给出了微分方程的特殊解——奇解与包络的求解方法。又由该定理的证明方法思路,类比证明了线性微分方程组与高阶线性微分方程解的存在性定理。由此可以知道微分方程解的存在性定理是微分方程解的存在性理论的基础。
在常微分方程的应用方面,我们不仅要会应用常微分方程这方面知识,还要知道如何将常微分方程的知识应用到实际生活中。在应用方面举例说明了数学建模中的动态模型——常微分方程模型,以及常微分方程的数值计算——欧拉方法和改进的欧拉方法,并且利用MATLAB求解常微分方程,简化了计算过程。在这些方面的应用说明了,常微分方程适用性较强,随着社会和科技的发展,更能够体现出常微分方程价值。
通过本课题的介绍,让我了解到理论与实际的结合,才能更好的处理问题,学好数学理论知识,是从理论数学转为应用数学的前提。

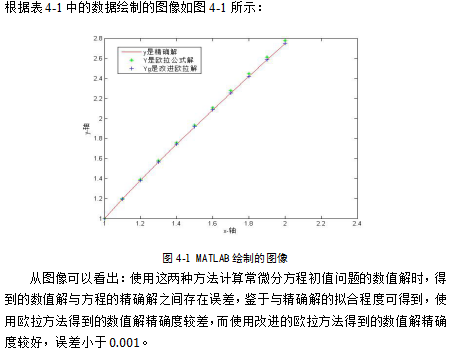
| 提示:此毕业设计论文完整版包含【论文】 作品编号:jskx0265,word全文:25页,合计:11000字 |
本信息与计算科学毕业设计论文作品由 毕业论文设计参考 [http://www.qflunwen.com] 征集整理——常微分方程解的存在性定理及应用(论文)!

 当前位置:
当前位置: 