复杂网络随着社会的进步发展了很多年，建立在学者们的工作基础上，普通的复杂连通网络可以被转换成与之对应的电网络。他们通过不断的研究，于是得到了电阻距离和基尔霍夫指数，它们在各个领域中都有十分广泛的应用。

在第二章中，介绍了电阻距离和基尔霍夫指数的概念，并且简单的叙述了电阻距离的计算方法。

在第三章中，首先介绍了一类双圈图的概念，接着分别进行了对一类双圈图的度和基尔霍夫指数的最小值和最大值进行了计算，然后得出相应的结论：

1.当一类双圈图第个顶点均分布在四边形同一对角线处时的度和基尔霍夫指数最小，此时求最小度和基尔霍夫指数的通项公式为：

2.当一类双圈图第个顶点依次连接在四边形同一非对角线处时的度和基尔霍夫指数最大，此时求最大度和基尔霍夫指数的的通项公式为：

在第四章中，先计算了一类双圈图的度积基尔霍夫指数的最小值和最大值，然后根据计算的结果和绘制的图形，得出了相应的结论：

1.当一类双圈图第个顶点均分布在四边形同一对角线处时的度积基尔霍夫指数最小，此时求出最小度积基尔霍夫指数的通项公式为：

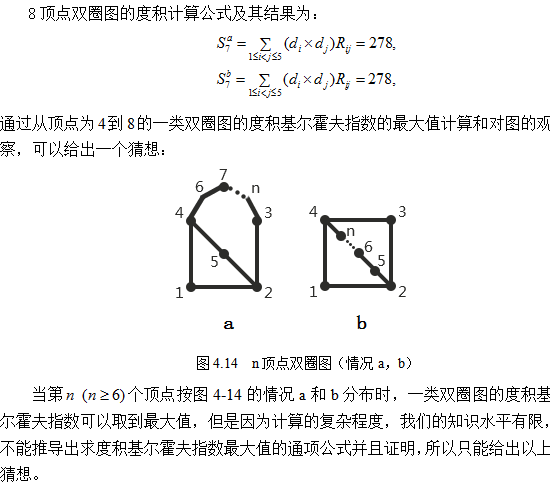
2.对于度积基尔霍夫指数的极大值，计算了4到8顶点双圈图的度积基尔霍夫指数，根据结果和对应的图形给出了一个猜想，如果当一类双圈图第个顶点按图4.14的其中一种情况分布时，就可以取到度积基尔霍夫指数的最大值。

在第五章中，介绍了本文中的主要的研究工作和结论，并提出了进一步的研究问题和方向。

......

选题的目的和意义

本文的主要研究目的是对双圈图的度和度积基尔霍夫指数极值的计算，电阻距离和基尔霍夫指数在提出来之后，就开始被广泛的进行研究，它们涉及到了很多领域，而且发掘出许多的研究成果[1]。电阻距离作为一个新的度量具有很多的优势，本事具有很多直观的性质吸引无很多人去研究，但是到目前为止，它的研究还不是很全面。所以电阻距离和基尔霍夫指数已经成为一门最为热门的研究科学之一，目前国内外对它们的研究都很火热[4]。在各个不同的领域中，它们的理论研究和应用研究都具有非常大的吸引力和挑战性，有着很广阔的应用前景[2]。因此对电阻距离和基尔霍夫指数的研究具有很重要的意义。

......

本文主要研究工作和结论

在本文中首先介绍了本课题了选题的目的和意义，接着对电阻距离和基尔霍夫指数的研究背景做了简单的叙述，并阐述了电阻距离和基尔霍夫指数的研究现状，接下来对本文中每个章节主要的研究内容做出详细的介绍。

在第二章中，介绍了电阻距离和基尔霍夫指数的概念，并且简单的说明了电阻距离的计算方法。

在第三章中，首先介绍了一类双圈图的概念，接着分别进行了对一类双圈图的度和基尔霍夫指数的最小值和最大值进行了计算，然后得出相应的结论：

1.当一类双圈图第个顶点均分布在四边形同一对角线处时的度和基尔霍夫指数最小，此时求最小度和基尔霍夫指数的通项公式为：

2.当一类双圈图第个顶点依次连接在四边形同一非对角线处时的度和基尔霍夫指数最大，此时求最大度和基尔霍夫指数的的通项公式为：

在第四章中，先计算了一类双圈图的度积基尔霍夫指数的最小值和最大值，然后根据计算的结果和绘制的图形，得出了相应的结论：

1.当一类双圈图第个顶点均分布在四边形同一对角线处时的度积基尔霍夫指数最小，此时求出最小度积基尔霍夫指数的通项公式为：

2.对于度积基尔霍夫指数的极大值，计算了4顶点到8顶点双圈图的度积基尔霍夫指数最大值，根据结果和对应的图形给出了一个猜想，如果当一类双圈图第个顶点按图4-14的其中一种情况分布时，就可以取到度积基尔霍夫指数的最大值。