论文围绕着Dirichlet级数及其相关问题展开讨论，在认真学习数论相关理论和研究方法的基础上，从一般Dirichlet 级数的建立，基本性质的讨论，到研究Dirichlet 级数的系数与此级数所给定的函数之间的关系，进一步利用所学的知识得到一些数论函数在特殊数列上的渐近分布性质，并利用 MATLAB 数学软件对研究对象进行数值验证。论文写作认真，表述清晰，推理严谨，文献翻译恰当，反映出该同学具有较好的学习和解决问题的能力。

本毕业设计论文主要围绕特殊数列的求和问题展开讨论，其中涉及平方补数列，k 次方补数列。为了给出特殊数列的渐近分布性质，我们通过给出不同数论函数在该类数列上的前 n 项和的渐近公式间接研究数列的分布性质，并以自然数列为对比数列，通过对于数论函数求和结果的比较来进一步分析该类数列的渐近性态。在文中所用到的数论函数有除数函数，除数和函数，除数和函数与其他数论函数的嵌套函数。本文中涉及到的知识点主要为解析数论和复变函数中的一些内容，主要包括利用佩龙公式将数列的求和问题转化为 Dirichlet 级数的积分问题，再利用 Dirichlet 级数的性质和 Riemann zeta-函数极点的性质将其转化为复变函数中求围道积分的问题, 最后通过计算复积分得到数列求和的渐近公式。并运用 MATLAB 软件编程计算准确的数列分布，再讲准确值和估计值绘图比较， 验证估计的准确性。最后在研究的过程中延伸并提出一般性问题：何种数论函数在 k 次方补数数列上可求和？这个问题较有难度，所以在本文中我们并没有得到一个精确的回答。只是通过在已经求得结果的计算过程中，总结公式化简的技巧， 发现规律，并证明其一般性。最终给这个问题给出了一个充分不必要的简单回答。

主要内容和成果

由上文所述，本文主要通过计算不同数论函数在给定数列上的前 n 项和来研究数列的性质。对于这个问题，已经有很多的研究结果，内容也非常丰富。所以在本文中只针对几种数论函数做一个简单的研究。

在本文的第二章中，介绍了本毕设研究所需要涉及的一些基础知识。

在本文的第三章中，首先计算了平方补数列上除数函数的前 n 项求和的估值，将该结果与自然数数列上除数函数的前 n 项求和估值做比较，可以得到平方补数列关于因数的特性，之后再从平方补数数列扩展到 k 次方补数数列，将问题一般化得到更一般性的结论。

在本文的第四章中，研究了 k 次方补数列在除数和函数，和更一般的 k 次方除数和函数上面的性质，并加入和其他的数论函数，研究了嵌套函数在数列上的性质。之后

延伸提出了有哪些数论函数在平方补数列上是可求和的问题。

在本文的第五章中，主要研究了之前提出的问题，并将计算过程中求和失败的数论函数做以讨论研究，从计算化简的方法中发现规律，最后得到一个充分但是不必要的条件。

在本文中，为了能更好的体现不同函数在数列上的关系，原自然数列与给定数列之间的差异比较，和为了方便一般性结论的证明。在估值中，主项只取阶数最大的一项作为最终结果。

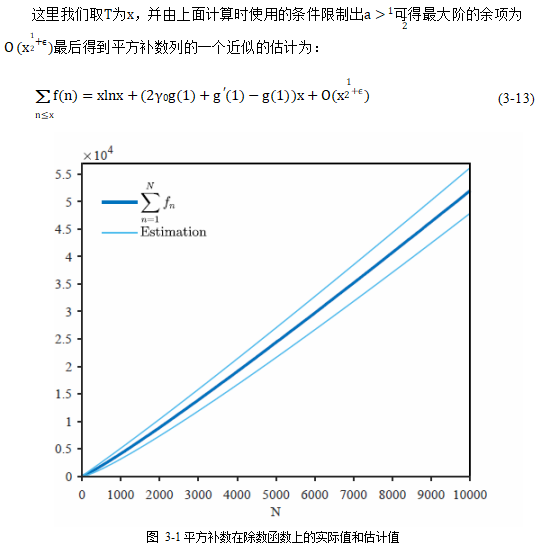
在研究计算估值的时候，也通过 MATLAB 绘制准确的分布图，并与计算结果做比较，验证计算的正确性。并直观的体现出不同数列之间的差异和联系。