一类具有阶段结构的SI模型的数值模拟
[关键词:阶段结构,SI模型,数值模拟] [热度 ]| 提示:此毕业设计论文完整版包含【论文】 作品编号:jskx0198,word全文:17页,合计:8000字 |

本文结构
本文的第一章绪论部分介绍了传染病研究的历史背景与特点以及数值模拟方法的历史背景与特点,并对文献中涉及到的内容进行了阐述;文章的第二章主要介绍了研究工作的基础与方法,并提出了本文将要研究的问题以及建立了相应的数学模型;在文章的第三章介绍了数值模拟方法的运用,将本文需要用到的龙格-库塔-芬尔格(Runge-Kutta-Fehlberg)方法进行了简单的阐述,并列举了一个利用MATLAB方法解常微分方程的例子为下面的模型数值模拟作了示范。在最后部分我们对模型进行了数值模拟,根据实验步骤得到了图象;在第四章我们对模型的数值模拟结果进行了分析,并将结果与理论模型分析的结果进行了比较,得到了我们想要得到的结论;第五章主要讨论了本文的研究意义。
模型的数值模拟
本文的模型模拟主要是运用MATLAB的龙格-库塔-芬尔格(Runge-Kutta-Fehlberg)方法来对二维竞争系统(2)的研究,具体的我们使用(4,5)阶的龙格-库塔-芬尔格方法来求解方程,利用此方法求解,得到两个种群与时间t之间的关系,进一步通过绘制图像来体现出两个种群的发展趋势和相互影响的程度,并通过方程内部的微调且代入,对其得到的不同结果进行比较分析,得出各个环境改变量对种群的影响。
模型数值模拟的结果分析
通过对前面一章的方程模型的数值模拟,我们通过对常数的取值的改变,得到了7个不同的图象。图中的绿线代表方程,蓝线代表方程。从这些图中我们可以看出,曲线在t时间内都全局稳定,根据各个常数的取值的不同,我们可以知道曲线的趋势也有所不同,曲线是幼年种群密度的改变趋势,它呈现一直递减状态;曲线是成年易感染者的种群密度的改变趋势,它呈现先递增,后递减的状态,表示易感染者的密度改变有一个高峰期,在达到高峰期就会趋于平稳。我们来看图1,幼年种群的密度的改变一直处于平缓下降的趋势,成年易感染者曲线也是比较柔和的,它先增后降,再跟另一条曲线一起渐近于0。除了图2的曲线是渐近与x=0.3外,其余的图形上的曲线在最后都渐近于0,这表示不管是幼年种群还是成年易感染者,它最后所呈现出来的种群密度的增长率都是接近于0,相当于种群的密度的改变不大,趋向于稳定。所有的图都表现出,,在t轴上的都是先处于反比状态,然后根据时间的推移渐渐处于正比状态,并最终趋于稳定。
数值模拟结果与理论研究结果的比较分析
有了数值模拟结果的分析,我们再来将数值模拟的结果与理论研究的结果进行一下比较。理论研究中的结果都是渐进稳定的,通过数值模拟所得的曲线模型,其图像的走向确实是渐进稳定的,这也证明了原理论研究结果的正确性。同时,我们通过图象也可以看出,传染病的传染率的改变,曲线的变化特别明显, 当=0.008时,曲线,的变化不是很明显,意味着种群的密度变化不是很大,而且它的增长并不渐近于0,它们是渐近于一个稳定的增长值;当=0.8时,曲线就是幼年种群的密度增长值急速下降到渐近于0,而的起伏很小,很快就渐近于0了。我们通过图象了解了改变常数的值,在一定程度上能改变图象中曲线的起伏,但并不能改变图象最后将趋于稳定的结局。所以由上面的分析,我们可以有理由相信原理论研究是正确的,原传染病模型是可行的。
研究的意义
本文是运用MATLAB数学软件将定性分析的数学模型通过具体的数据处理绘出图形,从而得到更直观、更形象的模型数据,将得到的模型数据与原来的定性分析进行比较,最终得到想要的结果。理论研究虽然是对研究课题进行定量分析的主要手段和有效方法,但是在研究过程中我们有时也需要用比较专业的数学知识进行描绘,这对研究者所要拥有的专业知识有很多的要求,所以对一般人来说是比较难完成的一向工程。并且模拟出来的模型方程比较笼统,也不易被读者所看懂。但数值模拟就不同了:数值模拟就其自身的直观、方便等特点,其计算的结果可以简单明白地得到,而且模拟出来的图像比较直观化,让研究者比较容易、清楚地得到各变量和影响因素的关系。它还可以根据分析的结果来修改原模型,或者修改某个常数量来改变模型的显示图象,使比较分析的过程更清晰;使之更接近于实际,最后所得到的结果也容易被读者看懂。本文通过MATLAB的数值模拟研究传染病模型的稳定性,进而我们可以用同样的方法去研究其他相似类型的模型。传染病模型的证明,在临床医学上意义甚大,如果掌握了传染病的传播规律和发病规律,那么将给我们带来的不少的福利。

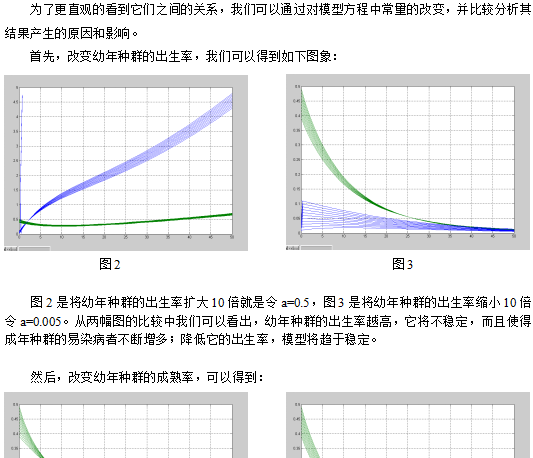
| 提示:此毕业设计论文完整版包含【论文】 作品编号:jskx0198,word全文:17页,合计:8000字 |
本信息与计算科学毕业设计论文作品由 毕业论文设计参考 [http://www.qflunwen.com] 征集整理——一类具有阶段结构的SI模型的数值模拟(论文)!

 当前位置:
当前位置: 