奇异分解技术用于信号分析的实践
[关键词:奇异分解,信号分析] [热度 ]| 提示:此毕业设计论文完整版包含【论文】 作品编号:txgc0588,word全文:33页,合计:10000字 |

研究内容
1)矩阵奇异值分解的概念
2)奇异值分解用于解线性方程组以及对得到的解进行去噪等优化处理(要求用MATLAB实现)
3)奇异值分解用于信号分析
4)进行仿真分析
拟解决的问题
用奇异值去解答一个线性的方程组(用MATLAB实现),优化所求解,并用这一个方程组所表达的信号意义对所求解进行检验。
信息的处理在现今这个高速发展的信息时代显得越发重要,基于奇异分解技术的信号分析在这方面的应用也是越来越广泛。复杂的,大容量的信息在数学模型上就是一个大的矩阵,对矩阵的计算就是对信号的分析与处理。奇异分解技术屏弃了传统的矩阵求逆法,通过对矩阵的因子分解把矩阵约化到相对简单的矩阵的特征值问题,取得了良好的数值稳定性。本论文对奇异值分解技术在理论和矩阵数值计算上进行了论述,利用MATLAB对相应信号进行了分析和仿真,并与传统求逆法进行了比较,以证明奇异分解技术的优越性。
结果的优化处理
由于在(-pi/10,pi/10),(-pi/15,pi/15), (-pi/30,pi/30)内结果是可以接受的,所以重点对(-pi/60,pi/60)内的仿真结果进行优化。在MATLAB的SVD()函数中得到的奇异值是统一按从大到小的顺序排列,排在最后的的奇异值最小,而与小奇异值相关联的特征可能在实际计算相似度时并不相关,将它们包括近来将降低相关性判断的精确度,相当于在这个用法变异中所引入的“噪音”,为了去掉这些不必要的“噪音”,我们将考虑剔除小的奇异值,保留下来的奇异值将表述方程的大有影响的特征。
所以进行优化的措施就是在解未知量的时候对奇异值进行取舍,在下面MATLAB文件的.m文件中采取如下两种措施对奇异值进行取舍:
1)直接对奇异值进行量的取舍,如改变for循环中的k=1:(n-0)为k=1:(n-1),去掉排在最后的一个奇异值(同时也是最小值的)。
2)设置针对奇异值的阀值1e-10,小于或者等于这个阀值的奇异值都不进入和式的计算中去。
与上图相比,本图中的红色曲线部分代表的值变小,和原始值相比较,变的太小,可以得出最后一个奇异值是不能舍掉的。同理,在SVD(2)里面的那个小的奇异值也是不能去掉的。不过,如果碰到后面的那个奇异值相对小到可以看做是信号噪声时,则可以去掉并且可以起到优化仿真结果的作用。

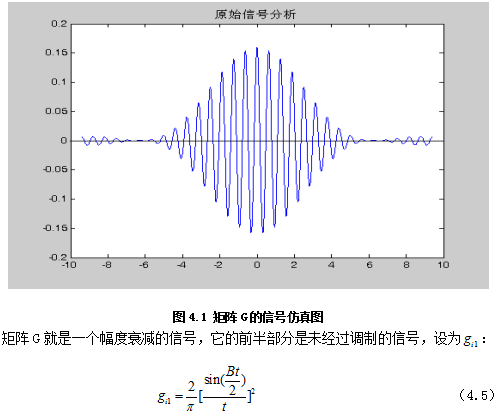
| 提示:此毕业设计论文完整版包含【论文】 作品编号:txgc0588,word全文:33页,合计:10000字 |
本通信工程毕业设计论文作品由 毕业论文设计参考 [http://www.qflunwen.com] 征集整理——奇异分解技术用于信号分析的实践(论文)!

 当前位置:
当前位置: 