论文简要介绍了回归支持向量理论和小波框架，根据框架理论导出了非均匀采样信号能够完全重建的条件，在此基础上分别利用框架迭代算法和回归支持向量机对平移不变空间中的同一个非均匀采样信号进行重建，重建结果表明若用回归支持向量机方法对平移不变空间中的非均匀采样的信号进行稳定重建则采样集必须满足由框架理论导出的完全重建条件；另外，文章也根据不规则小波框架的稳定性理论和不规则加权小波框架算法提出了针对非均匀采样信号重建的不规则加权小波框架共扼梯度算法，通过数值仿真实验和[相关文献中的算法进行比较，得到这种新算法在逼近误差与重建速度的方面有较大的优势。

由第四章中多次实验发现两种算法对该章4.15式给出的信号重建时间与迭代次数之间基本呈相同的线性关系，每迭代一次约0.02秒；两种算法的重建误差的方差并不是随着迭代次数的增加而减少，与迭代次数之间的关系曲线大致呈U字形，前面的迭代是逼近源信号，随着迭代次数的增加，计算中的舍入误差严重影响逼近效果，因此逼近效果与迭代次数之间并不呈正相关，由下图表5.2(由附录2程序  所得)可知，为了使两种算法都达到最好的逼近效果，用算法4.7要迭代15次左右，用算法4.9-4.13要迭代25次左右，且几乎在任何一次迭代后后种算法比前种算法的重建误差的方差都要小，即后种算法重建的信号比前种算法重建的信号要光滑的多，第四章图4.6，4.7也证明了这一点；由表5.2知，算法4.9-4.13迭代一次的重建误差的方差为0.0022，大约是7的迭代20次时的最优值0.0043的一半，因此实际应用中可将算法4.9-4.13迭代5次以下的结果作为重建信号，此时所需时间小于0.1020秒。多次实验发现对尺度的个数的选择需要折中，较少会使重建信号很不光滑，较多会增加计算时间，本例中取4个尺度比较合适；迭代过程中误差估计式4.8总是成立的，但(4.14)式在迭代次数较多时会被破坏。

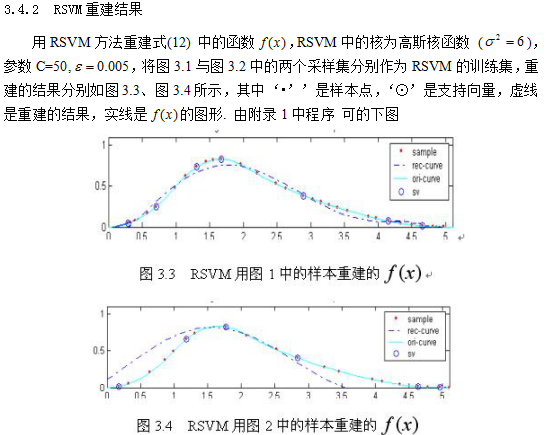
对于一个信号，如果它满足定理3.4或满足定义4.1.2中小波框架的条件，那么就能够通过迭代的方法稳定并且唯一得地重建。文章用框架算法和RSVM方法对是否满足定理3.4中条件的采样集分别进行了重建，并且比较了重建结果。实验结果表明，如果要用RSVM方法对非均匀采样的信号能进行稳定重建，那么其采样集也须满足定理3.4的条件，且此时重建信号比用迭代法重建信号的光滑程度有较大提高。由于仅由支持向量就可重建信号，因此RSVM将在信号的压缩传输中具有较大的优越性。另外，文章也对不规则加权小波框架共扼梯度算法和文献[5]所提到的最简单有效的不规则加权小波框架算法进行了比较，实验结果表明，无论是从计算速度还是重建精度来看，不规则加权小波框架共扼梯度算法都比其优越。

研究和解决的问题：

重建方法问题的实质就是函数逼近问题。从信号处理的角度来看，曲线的重建问题就是信号重建问题:一是当采样集满足什么条件时，信号能够由它在采样集上的采样值稳定而且唯一地重建；二是如何设计快速稳定的重建算法来重建信号。对非均匀采样集要满足怎样的条件，才能稳定重建信号，这一问题有广泛的应用背景，对该问题的研究既有理论意义又有实际价值。信息传输中的数据丢失、存储数据的硬件损坏、采样设备的限制等都会导致采样数据是非均匀的。近几年来非均匀采样的信号重建问题受到广泛关注。因此有必要对非均匀采样迭代重建方法进行深入的研究和进一步的了解。

采用的方法或技术路线：

（1）.先对已有的非均匀采样的实际成果进行学习，总结并且消化前人已经取得的成果，然后采用现代数学的分析方法对非均匀采样迭代重建方法进行理论研究,并用数学方法论证它在逻辑上的可行性。

（2）.对文章提出的非均匀采样信号的算法进行实际模拟演示，采用MATLAB数学软件对理论上取得的结论和成果进行编程模拟仿真，以验证结果的准确性。